雷达波形与信号

发表于   |   分类于   |  

雷达的分辨率

雷达波形$u(t)$的自相关函数主瓣宽度越窄，其距离分辨能力越强。即若要时间（距离）分辨率好，应选择这样的信号，即它通过匹配滤波器后应该输出很窄的主瓣波峰。这样的信号或是具有很短持续时间的脉冲，或是具有很宽频谱的宽带波形。

瑞利时间分辨率：$\delta_t = 1/B$，或等效地，瑞利距离分辨率：$\delta_r = c/{2B}$。

多普勒频率分辨率:$\delta_{fd} = 1/T$，或对目标径向速度分辨率:$\delta_v = \lambda / {2T}$。

总结：

  1. 雷达的距离/时间分辨率由雷达发射信号的带宽决定。 该带宽可以是瞬时的(如极窄的脉冲)，也可以是合成的(通过时间换取，如脉冲持续时间长的线性调频波)。在实际应用中，该宽带信号可是窄脉冲波形、线性调频波形、频率步进波形、随机或伪随机噪声波形及其他任何宽带调制信号。
  2. 雷达的速度/多普勒分辨率由信号的持续时间决定。 持续时间越长，分辨率越高。可通过发射持续时间长的脉冲或通过多个脉冲的相参积累等实现。

线性调频脉冲LFM

Linear Frequency Modulation，LFM。对雷达波形进行调频得到宽带信号，分为上变频和下变频。

该体制采用宽脉冲发射以提高发射的平均功率，保证足够大的作用距离；而接收时采用相应的脉冲压缩算法获得窄脉冲，以提高距离分辨率，较好的解决雷达作用距离与距离分辨率之间的矛盾。

LFM信号示意图.jpg

设线性调频信号为$s(t) = 1/\sqrt{t_p} rect(t/t_p)e^{j(\omega_c t+\pi \gamma t^2)}$
其中$\omega_c$为发射中心频率，$t_p$为脉冲宽度，$\gamma$为线性调频斜率，$B=\gamma t_p$。
包络调制函数为$u(t) = 1/\sqrt{t_p} rect(t/t_p)e^{(j\pi \gamma t^2)}$
随时间变化的频率函数为$f(t)=1/{2\pi}d/{dt} (\omega_c t + \pi \gamma t^2) = \omega_c/{2\pi}+\gamma t$

Matlab仿真代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
%%demo of chirp signal
T=20e-6;                          %pulse duration us
B=50e6;                           %chirp frequency modulation bandwidth MHz
K=B/T;                            %chirp slope
Fs=4*B;Ts=1/Fs;                   %sampling frequency and sample spacing
N=T/Ts;
fc=0;
t=linspace(-T/2,T/2,N);
St=exp(1i*pi*K*t.^2);                 %generate chirp signal
St=St.*exp(1i*2*pi*fc*t);
subplot(211)
plot(t*1e6,real(St));
xlabel('Time in u sec');
title('Real part of chirp signal');
grid on;
subplot(212)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St))));
xlabel('Frequency in MHz');
title('Magnitude spectrum of chirp signal');
grid on;

结果如下
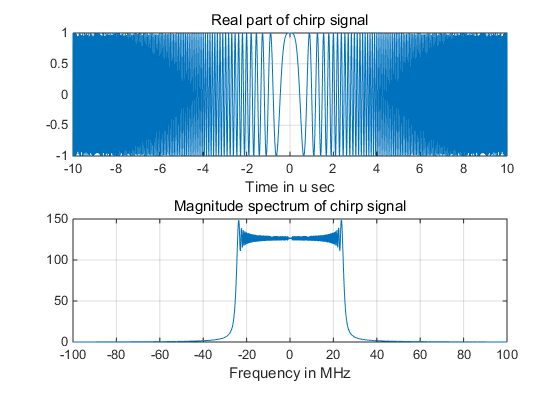
lfm信号仿真结果.png

脉冲压缩

线性调频斜率为$\gamma$、脉宽为$t_p$的脉冲，通过匹配滤波器后，时间分辨率为$1/\gamma t_p$。对于雷达接收机而言，相当于输入脉冲的宽度为$t_p$，输出脉冲宽的为$1/\gamma t_p = 1/B$，即输出与输入脉冲宽度之比为$1/\gamma t_p^2$。
在LFM雷达中，$\gamma t_p^2$通常称为时宽带宽积，且有$\gamma t_p^2 \gg 1$。
可见，接收机（匹配滤波器）的输出脉冲宽度在时间上被“压缩”，称之为脉冲压缩(Pulse compression)。
也就是说，为了获得线性调频信号的大带宽所对应的高级了分辨能力，必须对接收到的LFM宽脉冲回波进行压缩滤波处理（匹配滤波），使其变为窄脉冲。

实现上，数字方法有非递归滤波器（时域卷积），正-反DFT（频域分析），后者占用内存少、运算量小、速度快，更长用。

为了抑制旁瓣，减少虚警，常用加权处理。即将匹配滤波器的频率响应乘上某些适当的“窗函数”，在时域中相当于一系列加权函数组成的滤波器和匹配滤波器级联。

Reference: 《雷达系统及信息处理》